Campa-móchate !

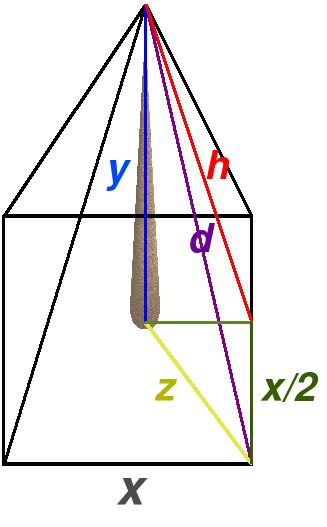
Se quiere fabricar una tienda de campaña de base cuadrada x y con una estaca central que formará cuatro triángulos isosceles, como se muestra en la figura.
Se dispone de 100 m2 de material.
¿Cuales son las dimensiones que determinan un volumen máximo? ¿Cuánto vale este?
dinamate.org
① Comenzamos planteando los 4 Teoremas de Pitágoras representativos en la figura mostrada :
(x/2)2+y2=h2
(x/2)2+h2=d2
(x/2)2+(x/2)2=z2
z2+y2=d2
de los cuales los tres últimos los dejamos para el uso del lector.
② Como el material esta formado por 4 triángulos :
100=4(xh/2)
de donde despejamos h=50/x
Con esta y la primera Pitagórica :
(x/2)2+y2=(50/x)2
y=√[100-x4]/2x
y como el volumen es el de un cono cuadrado :
V(x,h)=x2y/3 ; V(x)=x√[100-x4]/6
*Verifica por favor los detalles
③ Finalmente y con la derivada *Del producto:
V'(x)=-x4/3√[100-x4]+√[100-x4]/6
la que al igualarla a cero y resolver
(con productos cruzados)
2x4=100-x4
x=∜[100/3]
finalmente se puede verificar que :
y=√2x/2
V=√2∜(100/3)3/6
*Hazlo por favor!
<--Las aproximaciones4 se muestran a la izq.
*Ejercicio : calcula los valores exactos de d y z.
  Mueve los puntos del applet ↑ ►, o